Fractales.

“To iterate is human, to recurse divine.”

Si vamos a asociar imágenes con matemática, cada forma tiene su expresión, por ejemplo el círculo es una figura en la cual el radio es fijo, entonces podemos decir que:

Si r = a con a fijo, podemos dibujar un círculo.

Si queremos hacer un cuadrado, ¿qué sabemos de él? Es cuadrado, ok, esta hecho por 4 líneas. Si lo ponemos sobre una grilla es relativamente fácil, dado que a las líneas verticales de la grilla las podemos hacer coincidir con nuestro cuadrado. Entonces, entre a y b tenemos una franja que nos da el ancho (en el eje de abajo, el de las X) y si es cuadrado y no rectángulo, también tenemos entre a y b en el eje de las Y (el vertical) otra franja que nos da el alto. Así, ya tenemos nuestro cuadrado delimitado, es todo lo de X que esta entre a y b y lo mismo para Y. De esta manera: 

a < x < b  y  a < y < b son las ecuaciones que definen nuestro cuadrado.

Ahora sabemos que podemos dibujar cualquier forma que querramos con una ecuación. Algunas son simples, otras no, pero así sean conexas o tengan picos o sean como te puedas imaginar, generalmente hay una ecuación (nadie dijo que sea fácil ni que sepamos cuál es) que la parametriza.

Montañas en el Tibet

Todo muy lindo hasta acá, pero qué pasa cuando tenemos una ecuación recursiva, en la que el valor siguiente está definido por el valor anterior, posiblemente les suene la serie de Fibonacci. Fibonacci toma el primer punto y le suma el segundo y eso da el tercero. De manera que empezás con 0 y 1 y sabés que el tercero es 1, el 4to es 2 porque suma 1+1, el 5to es 3 y el 6to es 5 (3+2). ¿Demasiados números? Acá hay una foto de fractales naturales para que no me odien.

Si tomamos una barra cualquiera, la partimos en 3 y nos quedamos con los bordes, eso representa una función que se puede aplicar a cualquier barra, en particular a los pedazos de barra que quedaron de los bordes de la barra grande. Cada uno es ahora una barra más chica que uno puede volver a partir en 3 repitiendo el proceso (a esto se le llama Iteración). Si hacemos de eso una imagen y la repetimos varias veces, tenemos el set de Cantor, que es de.... sí, un flaco que se llamaba Cantor.

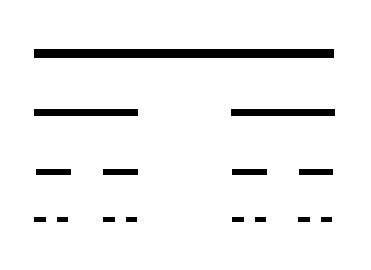Fractals and stuff

Como se ve en la imagen, este set se puede repetir infinitamente y cada uno de ellos es similar al original, si tomás la barrita de la izquierda y le haces un "zoom" va a tener la misma estructura que el diseño original. Eso, exactamente eso es un fractal.

Hay varios tipos de fractales, el de arriba es idéntico al original en cada etapa, no importa cuántas iteraciones uno realize,  es el nivel de "autosimilaridad" de cada fractal lo que lo hace único. 

Por ejemplo, la siguiente imagen se arma a partir de la regla "en cada nodo, salen 3 líneas a 120 grados".

En la naturaleza hay montones de cosas que se reproducen como un fractal, claramente no son infinitos como su analogía matemática porque no hay manera de que un brócoli tenga infinitas partes, pero son técnicamente lo mismo. En la imagen aparece un brócoli que está armado como un fractal, un helecho y una formación de nubes, todas que siguen este patrón de autosimilariadad a varios niveles. Si quieren más imágenes, acá hay.